Polynomial Regression In Machine Learning: “Data is the new oil,” and machine learning is the engine that drives its value. Among the many techniques used to make sense of data, polynomial regression in machine learning plays a vital role in solving complex prediction problems that linear regression can’t handle.

If you’ve ever seen a curve fitting perfectly through a scattered set of data points, you’ve already witnessed polynomial regression in action. But what exactly is it? How does it work? And why is it important? Let’s explore step by step, shall we?

What is Polynomial Regression in Machine Learning?

In simple terms, polynomial regression in machine learning is an extension of linear regression. While linear regression models the relationship between independent and dependent variables using a straight line, polynomial regression fits a curved line (or curve) to capture more complex patterns in data. It helps when your data doesn’t follow a straight-line trend but shows curves or fluctuations.

Definition: Polynomial regression is a type of regression technique where the relationship between variables is expressed as an nth degree polynomial.

Mathematically,

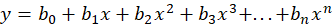
Here, are the coefficients, and is the degree of the polynomial.

In short:

• Linear regression: Straight line
• Polynomial regression: Curved line

How Does Polynomial Regression Work?

Let’s simplify this.

1. Start with Linear Regression: Polynomial regression begins like linear regression, where the model tries to find a line that best fits the data.
2. Add Higher-Degree Terms: It adds powers of the independent variable (like etc.) to capture the curve in the data.
3. Train the Model: Using algorithms such as Ordinary Least Squares (OLS), the model calculates coefficients that minimize the difference between predicted and actual values.
4. Evaluate the Model: Once trained, it checks performance metrics like R² (R-squared), Mean Squared Error (MSE), or Root Mean Squared Error (RMSE).

Polynomial regression fits the data by bending the line to follow its natural shape.

Polynomial Regression Example in Machine Learning

Let’s look at a basic polynomial regression example in machine learning. Suppose you are predicting the price of houses based on their area. If the data shows that prices rise quickly at first and then slow down, a straight line (linear regression) won’t fit properly.

Instead, by applying polynomial regression in machine learning, we can use a second- or third-degree polynomial that bends and fits the data more accurately. This kind of model is especially useful in cases like:

• Predicting sales trends over time
• Estimating growth rates
• Analyzing population data
• Forecasting temperature or pollution levels

Example: A dataset showing car engine size (x) vs. fuel consumption (y) will often form a curve. Linear regression fails, but polynomial regression captures it perfectly.

Linear and Polynomial Regression: The Key Difference

Let’s clear one common confusion, the difference between linear and polynomial regression.

Features	Linear Regression	Polynomial Regression
Model Type	Straight Line	Curved Line
Equation	y = b0 + b1x	y = b0 + b1x + b2x² + …
Use Case	Data with linear relationship	Data with curved or non-linear trend
Complexity	Simple	Moderate to complex
Accuracy	Limited for non-linear data	Better for non-linear data

In short, linear and polynomial regression differ mainly in their ability to capture curvature in data. Polynomial regression provides flexibility when data patterns are non-linear.

Polynomial Regression for Multiple Variables

So far, we discussed a single variable. But what if you have multiple features, like house area, number of rooms, and location score?

That’s where polynomial regression for multiple variables comes into play. It extends the same concept to more than one independent variable. The model includes not just higher powers of each variable but also their combinations (like , , etc.).

This helps in building more accurate and real-world predictive models, especially in complex domains like:

• Climate prediction
• Financial modeling
• Marketing and sales forecasting

Example: Predicting demand using both “price” and “advertising spend” as input features.

Advantages of Polynomial Regression in Machine Learning

1. Captures non-linear patterns: Works well when data is curved.
2. Flexible: Can fit data that linear models cannot.
3. Improved accuracy: Gives better predictions in many real-world cases.
4. Easy to implement: Can be done using libraries like Scikit-learn in Python.

Limitations of Polynomial Regression

1. Overfitting: If the degree is too high, the model fits noise instead of trend.
2. Computation: Higher-degree models can become complex.
3. Extrapolation Issues: Predictions outside the range of training data may be unreliable.

“The trick is to find the right balance, not too simple, not too complex.”

When to Use Polynomial Regression in Machine Learning

Ask yourself:

• Is your data showing a curved trend?
• Does linear regression give poor accuracy?
• Do residual plots show patterns (instead of randomness)?

If yes, then polynomial regression in machine learning is likely the right approach.

Read more: Resolution in Artificial Intelligence Examples Explained Simply

On A Final Note…

Polynomial regression in machine learning is like giving your model “flexibility” to follow the natural shape of your data.

“Data rarely behaves in straight lines; polynomial regression teaches your model to bend without breaking.”

Whether you are predicting sales, growth, or environmental changes, this method bridges the gap between simple linear models and complex non-linear systems. So next time your linear regression graph looks off, remember, maybe your data just wants a little curve!

FAQs